Chap.2 Point bonding at a partial contact among solids
2.1 Point bonding by short-range force among solid particles
Although universal gravitation is not neutralized and has a far-reaching effect (Eq.3), the short-range force of Coulomb force (Eq.1) is very stronger than the universal gravitation in the atomic-level distances.The substance is not glued together by the long-range force of universal gravitation. The Coulomb force (Eq.2) is 34 orders of magnitude stronger than that of gravitation. The Coulomb force acts on charged particles, and cancels each other out with positive and negative charges, so the effect effects at distance of about the atomic level.
FG = G・(mp)2/d2 ; G=6.67x10-11 [N・m2・kg-2], mp=1.66x10-27 [kg] (1)
FC = k・(qp)2/d2 ; k=9.0x109 [N・m2・C-2], qp = 1.6x10-19[C] (2)
FG / FC = 1.84x10-64/(2.3x10-28) = 8x10-35. (3)
Cosmic dust masses are clusters of fine particles and are constructed by short-range forces.
The energy of the reaction in which free atoms such as hydrogen and oxygen form covalent bonds is 50~110 kcal/mol. The energy of the ionic bond is in the range of 3~7 kcal/mol. The energy of the van der Waals bond, which is a weak bond, is 1~2 kcal/mol. In contrast, the energy of thermal motion of molecule at 25°C is 0.6 kcal/mol. Therefore, even if a gas molecule collides with a cosmic dust in space, most of the molecule bounce back. However, when fine particles come into contact with fine particles, there occurs a local point where atoms approach other atom about the size of an atom, and the electrons of the atom interact with the electrons of other atoms. The interaction generates high energy states and low energy states, and the state change to the low energy states. Fig.1 indicates the energy of atoms per atom that decreases depending on the bond state.
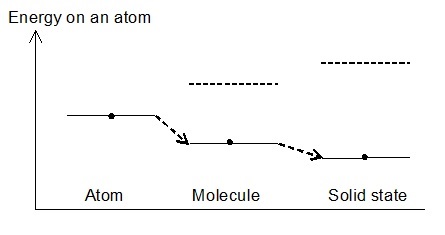
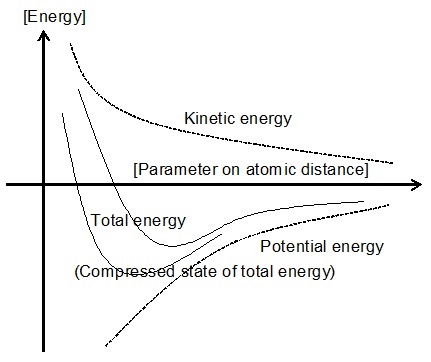
Fig.1 Energy state that changes depending on the binding state Fig.2 Decrease in energy due to reduction of interatomic distance
Fig.2. shows the energy change when compression and expansion are performed
without changing the quantum state of the substance. This illustrates a
condition of equilibrium called the Virial theorem, which gives the equilibrium
state in which the sum of potential energy and kinetic energy is the lowest.
The product of momentum space and metric space does not change as the condition
of quantum state, and according to this condition, the kinetic energy increases
inversely proportionally when the spatial distance is compressed if the
product of pressure and volume is not changed in an ideal gas. The potential
energy of attraction acting on the nucleus and electrons decreases in inverse
proportion to size, while the kinetic energy increases inversely proportionally
to the square of size. Therefore, the lowest energy state is given with
kinetic energy at half the potential energy. (last modified Feb/27 2023)
index -2.1-